Baisser la température de son logement fait-il vraiment baisser la facture ?

Calculer le bilan énergétique d’un logement, c’est avant tout estimer le montant des déperditions thermiques, c’est-à-dire le montant d’énergie s’échappant par les différentes parois du logement. Vous avez d’ailleurs surement déjà entendu parler des passoires thermiques, ces logements qui laissent tellement échapper l’énergie qu’ils sont qualifiés de passoires (comme leur nom l'indique 😉).

Il est important de différentier le calcul des déperditions thermiques de celui de la performance du chauffage. En effet, les déperditions, en plus de dépendre du type de chauffage de votre logement, sont aussi influencées par les caractéristiques de l’habitation.

Nous nous concentrerons ici sur l’estimation des pertes en énergie thermique du logement, dont le calcul est le même pour tous les types d'appareils de chauffage (électrique, gaz naturel, bio méthane, fioul, propane, bois de chauffage ou granule de bois).

Elle a été introduite en 1974 à la suite du premier choc pétrolier par la réglementation thermique française (RT1974). Le but était de mesurer la performance énergétique des logements pour permettre de réduire la consommation d’au moins 25%, soit environ 75 kWh/m² par an et par foyer.

Ainsi, le calcul de la déperdition thermique du logement via cette méthode est le suivant : DT = G.V.𝚫T

Le coefficient G, lorsqu’il n’est pas connu, peut être estimé en utilisant des valeurs de référence obtenues à l’aide des moyennes de plusieurs valeurs observées :

Logiquement, ces déperditions varient en fonction de la température intérieure (la température sur laquelle les thermostats de vos appareils de chauffage sont réglés).

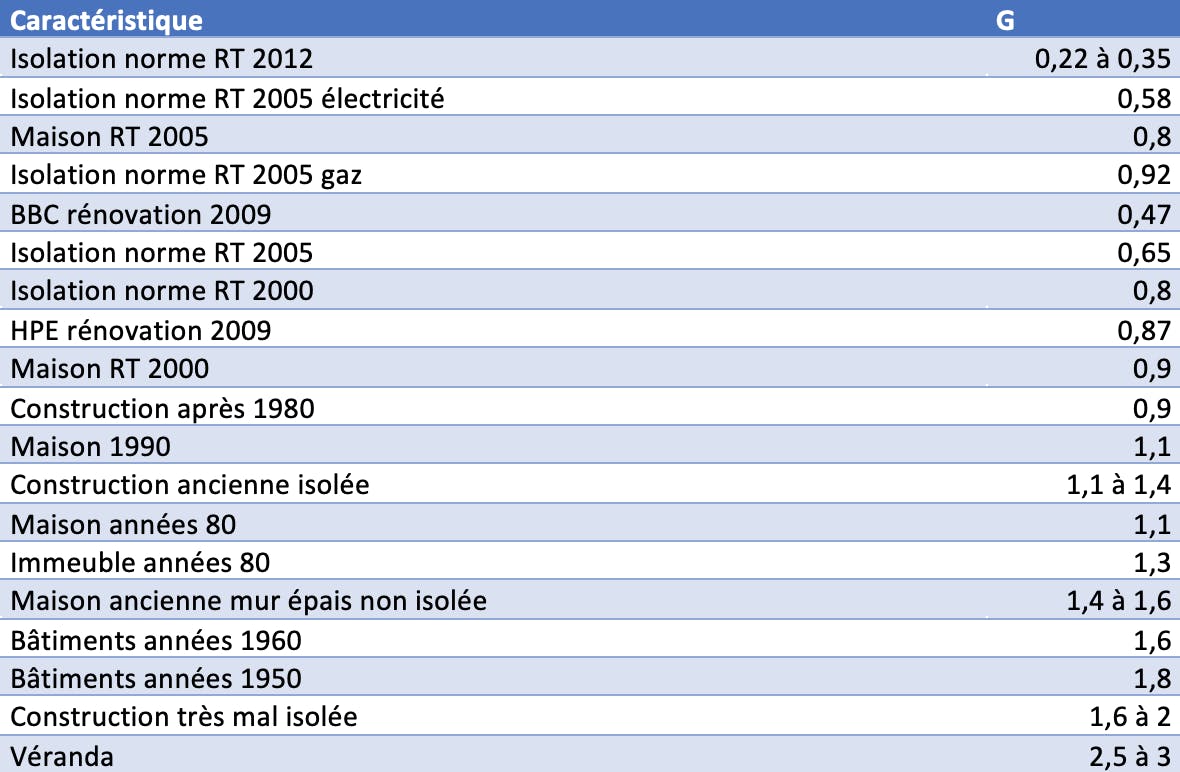
Pour cela, il faut calculer la dérivée partielle par la température intérieure des déperditions thermiques selon les deux méthodes vues précédemment. La dérivée partielle d’une fonction par une variable revient à calculer la variation de la fonction lorsque la variable explicative varie d’une unité. Dans notre cas, cela revient à déterminer quelle est la variation de la déperdition thermique lorsque l’on augmente la température intérieure d’un degré.

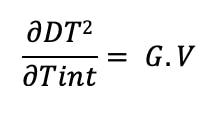
On remarque que pour un logement donné, la dérivée est constante.

On peut maintenant calculer l’augmentation en pourcentage (P) de la déperdition lorsque l’on augmente la température intérieure d’un degré, ce qui revient à diviser la dérivée de la déperdition thermique par elle-même.

En effet, comme la dérivée représente le volume supplémentaire de déperdition, diviser cette valeur par la déperdition de départ revient à calculer le taux de hausse de cette dernière.

Ainsi, on peut estimer la hausse de la déperdition thermique, lorsque l’on augmente la température intérieure d’un degré au ratio de 1 sur la différence entre la température de thermostat et la température extérieure.

Prenons un exemple concret pour illustrer ces calculs :

Calculons la déperdition par la méthode G : DT = G.V.𝚫T = 1,3 x 60 x (19-7) = 936W

Calculons désormais cette même déperdition si le chauffage était réglé sur 20°C, soit un degré de plus : DT = G.V.𝚫T = 0,35 x 60 x (20-7) = 1014W

L’augmentation de la déperdition est donc de 8,3%

Appliquons désormais la formule déterminée précédemment :

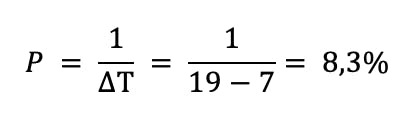
Le résultat de la formule nous montre que seuls les volumes de déperditions dépendent des caractéristiques du logement, en revanche, la proportion d’économie en énergie réalisée lorsque l’on modifie la température intérieure sera toujours la même et ne dépend que de la température extérieure et celle du thermostat.

Intéressant ces calculs n’est-ce-pas ? Pour que cela vous parle plus, il est possible de calculer les économies que la baisse du chauffage d’un degré seulement représenteraient.

Si on considère que le chauffage fonctionne 5 mois sur l’année et que le prix du kWh est à 0,18€. Le volume de perte supplémentaire lors du passage de 19 à 20°C étant de 78W, on peut calculer l’économie réalisée lors du passage de 20 à 19°C :

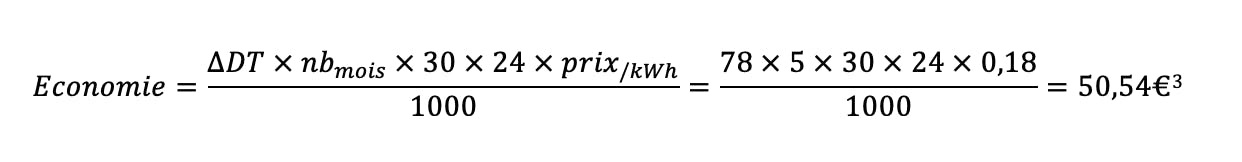
Environ 50€ d’économies réalisées, et ce sur une seule pièce, pas mal non ?

Calculer mes économies à partir de mon diagnostic de performance énergétique (DPE)

Nous vous proposons également une approximation des économies réalisables à partir de votre diagnostic de performance énergétique. Celui-ci vous donne une note de A à G calculée en fonction de la consommation du logement par m2 par an.

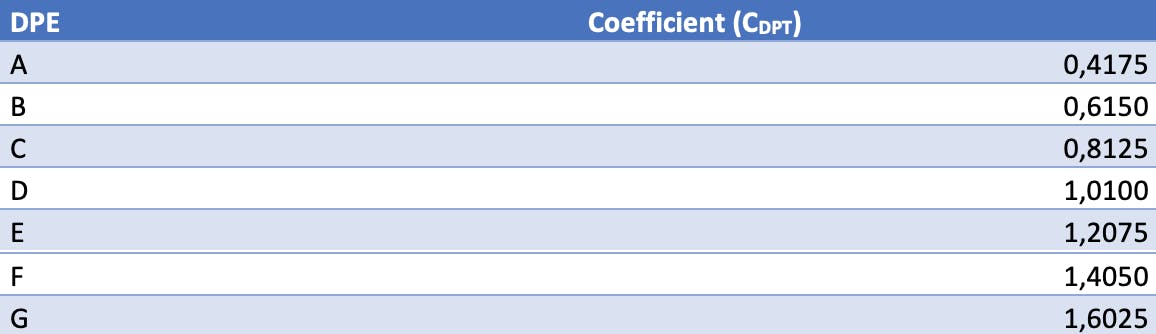
Pour donner une estimation du coefficient de déperditions volumiques par degré, on effectue une répartition linéaire sur l’intervalle des valeurs prise par le coefficient G (de 0,22 à 1,8) que l’on répartit de manière croissante entre les notes A et G.

Cela nous donne ce tableau :

Le calcul à effectuer est alors le même que celui de la méthode G :

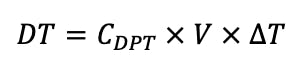
Si on reprend les données de l’exemple précédent et que l’on considère que le logement est noté E, la déperdition thermique sera alors de : DT = 1,2075 x 60 x (19-7) = 869,4W

On décide de réaliser des travaux d’isolation qui permettent de passer à une note de B, calculons les économies réalisées :

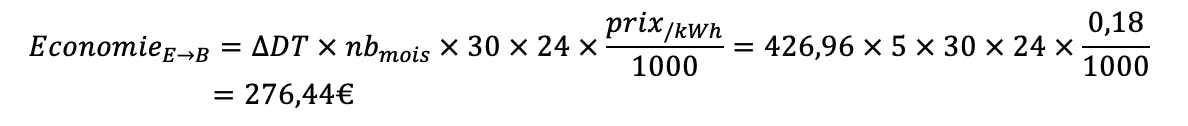
Un peu plus de 275€ d’économies réalisées par an ! (Soit environ 4,6€ par m³)

Il est cependant possible de jouer sur deux variables qui pourront vous permettre de diminuer les pertes énergétiques et ainsi réaliser des économies :

Si oui, voici une sélection d'articles pour choisir le thermostat connecté idéal et bien le régler pour toujours plus d'économies 😉 :

¹ : La norme voudrait que l’on exprime les degrés en Kelvin (K) qui est l’unité de base pour le domaine de la température. Or, comme la formule fait intervenir un écart de température, nous pouvons utiliser les Kelvin ou les degrés Celsius étant donné la règle de conversion : °C + 273,15 = °K.

² : c'est la notation mathématique pour exprimer la dérivée partielle de la fonction DT par la variable Tint

³ : On notera que l’économie est proportionnelle au nombre de degrés réduits. Pour rester sur l’exemple, si la température de départ était de 22°C, l’économie réalisée après le passage à 19°C aurait été de 3 fois 50,54€ soit 151,62€.